자료구조 - 균형 이진 탐색 트리(Balanced Binary Search Tree)
1. 균형 이진 탐색 트리
- 노드의 삽입과 삭제가 일어날 때, 균형을 유지하도록 하는 트리
- 종류 : AVL 트리, Red-Black 트리
2. AVL 트리
- 노드가 삽입, 삭제될 때 트리의 균형을 체크하고 유지하는 트리
- BF(Balance Factor) : 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이
- 각 노드의 BF를 [-1, 0, 1] 만 가지게 하여 균형을 유지
3. 리밸런싱
균형이 깨진 경우
- BF가 '+'이면 왼쪽 서브 트리에 이상이 있음
- BF가 '-'이면 오른쪽 서브 트리에 이상이 있음
회전 연산
- 단순 회전 : LL,RR
- 이중 회전 : LR, RL
- LL (Left - Left)
- 오른쪽 방향으로 1회 회전

- RR (Right-Right)
- 왼쪽 방향으로 1회 회전

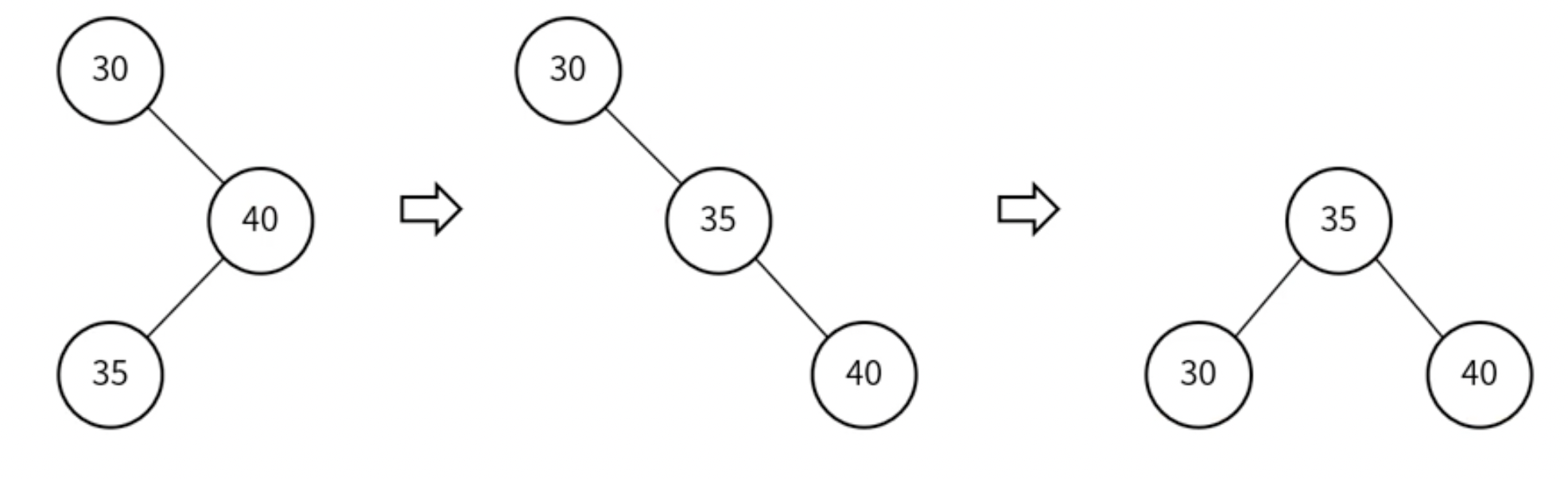
- LR (Left - Right)
- RR회전 후 LL회전

- RL (Right - Left)
- LL회전 후 RR회전
4-1. AVL트리 - 삽입 구현
- 각 회전 연산에 대한 메소드 생성 후 삽입 함수를 재귀하며 각 노드들을 리밸런싱 해줌
// AVL트리 - 삽입
import java.util.LinkedList;
import java.util.Queue;
class Node{
int key;
int height;
Node left;
Node right;
public Node( int key, Node left, Node right) {
this.height = 0;
this.left = left;
this.right = right;
this.key = key;
}
}
class AVLTree {
Node head;
public int height(Node node){
if (node == null){
return -1;
}
return node.height;
}
public Node rightRotate(Node node){
Node lNode = node.left;
node.left = lNode.right;
lNode.right = node;
node.height = Math.max(height(node.left), height(node.right)) + 1;
lNode.height = Math.max(height(lNode.left), height(lNode.right)) + 1;
return lNode;
}
public Node leftRotate(Node node){
Node rNode = node.right;
node.right = rNode.left;
rNode.left = node;
node.height = Math.max(height(node.left), height(node.right)) + 1;
rNode.height = Math.max(height(rNode.left), height(rNode.right)) + 1;
return rNode;
}
public Node lrRotate(Node node){
node.left = leftRotate(node.left);
return rightRotate(node);
}
public Node rlRotate(Node node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
public int getBalance(Node node){
if (node == null){
return 0;
}
return height(node.left) - height(node.right);
}
public void insert(int key){
this.head = insert(this.head, key);
}
public Node insert(Node node, int key){
if (node == null){
return new Node(key,null,null);
}
if (node.key > key){
node.left = insert(node.left, key);
}else {
node.right = insert(node.right, key);
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
int balance = getBalance(node);
if (balance > 1 && key < node.left.key){
return rightRotate(node);
} else if (balance < -1 && key > node.right.key) {
return leftRotate(node);
} else if (balance > 1 && key > node.left.key) {
return lrRotate(node);
} else if (balance <-1 && key < node.right.key) {
return rlRotate(node);
}
return node;
}
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList();
queue.add(node);
while (!queue.isEmpty()){
Node cur = queue.poll();
if (cur.left != null){
queue.add(cur.left);
}
if (cur.right != null){
queue.add(cur.right);
}
System.out.print(cur.key + " ");
}
System.out.println();
}
}
public class Main {
public static void main(String[] args) {
AVLTree avl = new AVLTree();
// Insert
avl.insert(30);
avl.insert(20);
avl.insert(10);
avl.levelOrder(avl.head); // LL
avl.insert(40);
avl.insert(50);
avl.levelOrder(avl.head); // RR
avl.insert(5);
avl.insert(7);
avl.levelOrder(avl.head); // LR
avl.insert(60);
avl.insert(55);
avl.levelOrder(avl.head); // RL
}
}
4-2. AVL 트리 - 삭제 구현
- 위의 클래스를 상속 받아 받은 키 값과 일치하는 노드를 찾음
- 찾은 노드의 자식 노드의 개수에 따라 값을 삭제 시킴
- 그 노드의 높이를 새로 설정하고 리밸런싱을 해줌

// AVL 트리 - 삭제
class AVLTree2 extends AVLTree{
public void delete(int key){
this.head = delete(this.head, key);
}
public Node delete(Node node, int key){
if (node == null){
return null;
}
if (node.key > key){
node.left = delete(node.left, key);
} else if (node.key < key) {
node.right = delete(node.right, key);
} else {
if (node.left == null){
return node.right;
} else if (node.right == null) {
return node.left;
} else {
Node successor = node.left;
Node predecessor = node;
while (successor.right != null){
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
node.key = successor.key;
}
}
node.height = Math.max(height(node.left), height(node.right)) + 1;
int balance = getBalance(node);
if (balance > 1 && getBalance(node.left) > 0){
System.out.println("LL");
return rightRotate(node);
} else if (balance < -1 && getBalance(node.right) < 0) {
System.out.println("RR");
return leftRotate(node);
} else if (balance > 1 && getBalance(node.left) < 0) {
System.out.println("lr");
return lrRotate(node);
} else if (balance < -1 && getBalance(node.right) >0) {
System.out.println("rl");
return rlRotate(node);
}
return node;
}
}
public class Practice1 {
public static void main(String[] args) {
AVLTree2 avl = new AVLTree2();
avl.insert(30);
avl.insert(20);
avl.insert(40);
avl.insert(10);
avl.levelOrder(avl.head);
avl.delete(40);
avl.levelOrder(avl.head); // LL
avl.insert(40);
avl.delete(10);
avl.levelOrder(avl.head); // RR
avl.insert(25);
avl.delete(40);
avl.levelOrder(avl.head); // LR
avl.insert(27);
avl.delete(20);
avl.levelOrder(avl.head); // RL
}
}'자료구조' 카테고리의 다른 글
| 자료구조 - 그래프(Graph) (0) | 2023.01.03 |
|---|---|
| 자료구조 - 이진탐색트리(Red - Black Tree) (0) | 2023.01.02 |
| 자료구조 - 이진 탐색 트리(Binary Search Tree) (0) | 2022.12.30 |
| 자료구조 - 이진 트리(Binary Tree) (0) | 2022.12.29 |
| 자료구조 - 연습문제 (0) | 2022.12.26 |



