자료구조 - 이진탐색트리(Red - Black Tree)
1. Red - Black Tree
조건
- root 노드와 leaf 노드의 색은 black
- red 색 노드의 자식은 black (double red 불가능)
- 모든 leaf 노드에서 root 노드까지 가는 경로의 black 노드의 수는 같음
- 조건이 깨지는 상황에서 리밸런싱
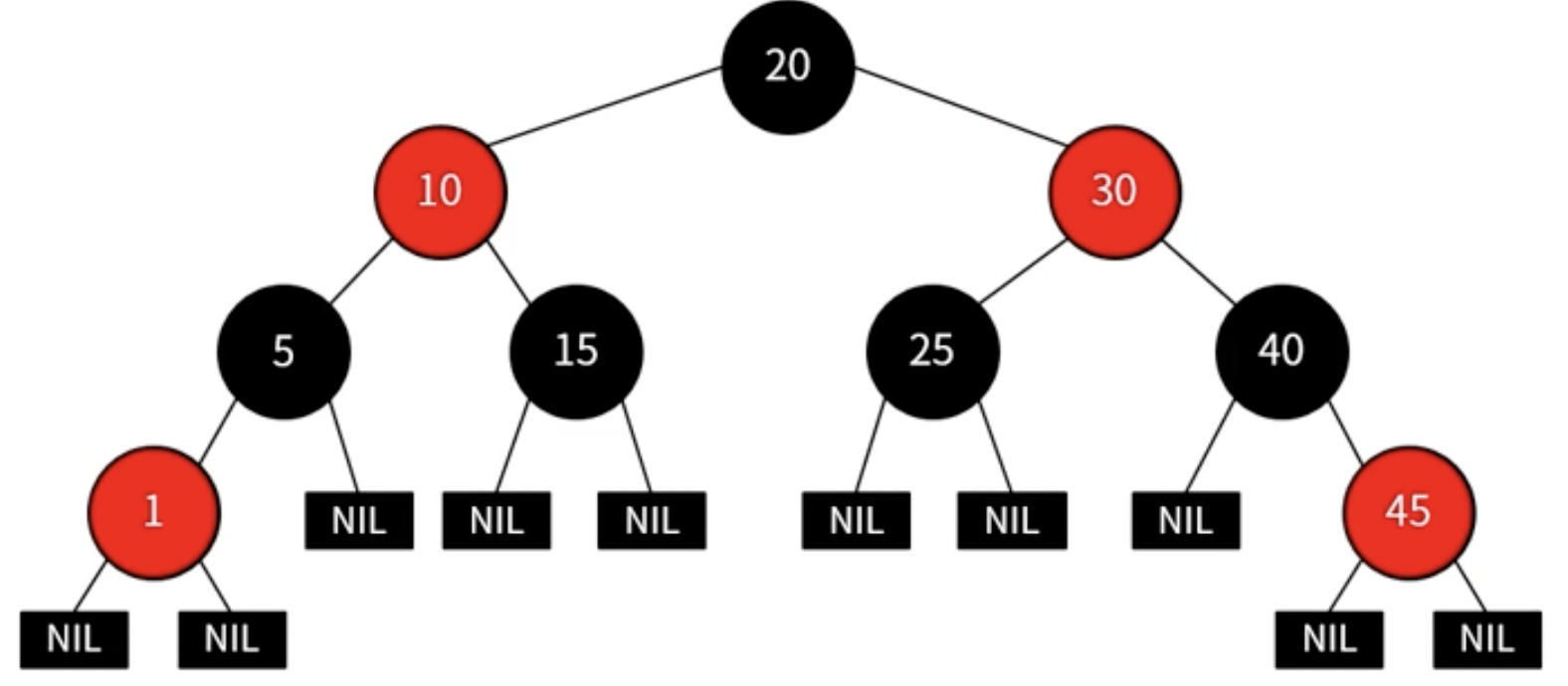
삽입
노드 삽입 후 double red 발생
- case 1 - 부모 노드의 형제 노드가 red 일 때
- Recoloring 진행
- 삽입한 노드의 부모와 부모의 형제 노드를 모두 black으로 변경
- 부모의 부모 노드를 red로 변경
- 부모의 부모 노드가 root 인지에 따라 조정 진행 (root 라면 검정으로 변경, 아니면 부모 노드의 색에 따라 조정)

- case 2 - 부모 노드의 형제노드가 black이거나 없을 때
- Restructuring 진행
- 조정 대상 : 삽입한 노드, 부모 노드, 부모의 부모 노드
- 조정 대상 노드들을 오름차순으로 정렬
- 가운데 노드를 부모 노드로 선정하고 black으로 변경
- 나머지 두 노드를 자식 노드로 두고 red로 변경

LL일 경우 : 오른쪽 회전 -> 부모 노드 검정 , 자식 노드 빨강

LR일 경우 : LR 회전 후 -> 부모 노드 검정, 자식 노드 빨강
삭제
- 기본
- 삭제 대상 노드가 black이고 그 자리에 red가 오는 경우
- 해당 자리로 오는 노드를 black으로 변경

- 이중 흑색 1(Double Black case1)
- 삭제 노드가 black, 그 자리에 black이 오는 경우 이중 흑색 노드의 형제 노드가 black이고, 형제의 양쪽 자식이 블랙인 경우
- 형제 노드를 red로 변경
- 이중 흑색 노드의 검은색 1개를 부모 노드로 전달
- 부모가 root가 아닌 이중 흑색 노드가 되면 해당 case반복 진행

- 이중 흑색 2(Double Black case2)
- 이중 흑색 노드의 형제 노드가 red인 경우
- 형제 노드를 black으로 변경
- 부모 노드를 red 로 변경
- 부모 노드를 기준으로 왼쪽으로 회전
- 그 다음 이중 흑색 case에 따라 진행

- 이중 흑색 3-1(Double Black case3-1)
- 이중 흑색 노드의 형제 노드가 black이고, 오른쪽 자식이 red인 경우
- 부모 노드와 형제 노드의 오른쪽 자식 노드를 black으로 변경
- 부모 노드를 중심으로 왼쪽으로 회전

- 이중 흑색 3-2(Double Black case3-2)
- 이중 흑색 노드의 형제 노드가 black이고, 왼쪽 자식이 red인 경우
- 형제 노드를 red로 변경, 형제노드의 왼쪽 자식 노드를 black으로 변경
- 형제 노드를 기준으로 오른쪽으로 회전
- 이중 흑색 case 3-1 진행
2. Red-Black Tree 와 AVL Tree 비교
- 알고리즘 시간 복잡도
- 둘 다 O(logN) - 균형 수준
- AVL 트리가 Red-Black 트리보다 좀 더 엄격하게 균형을 잡음
- Red-Black 트리는 색으로 구분하는 경우로 인해 회전 수가 감소 - 실 사용시
- Tree 체계가 잡힌 후, 탐색이 많은 경우에는 AVL 트리가 유리
- 삽입, 삭제가 빈번한 경우에는 Red-Black 트리가 유리
3. Red-Black 트리 - 삽입 구현
- 회전을 구현할 때 트리를 그려보면서 하나씩 작성하기
// 비선형 자료구조 - 이진 탐색 트리_3
// Red-Black 트리 - 삽입
import java.util.LinkedList;
import java.util.Queue;
class Node{
int key;
int color;
Node left;
Node right;
Node parent;
public Node(int key, int color, Node left, Node right, Node parent) {
this.key = key;
this.color = color;
this.left = left;
this.right = right;
this.parent = parent;
}
}
class RedBlackTree{
final int black = 0;
final int red = 1;
Node checkNode;
Node head;
public void insert(int key){
if (this.head == null){
this.head = new Node(key, black, null,null,null);
} else {
Node cur = this.head;
// 노드를 올바른 위치에 삽입
while (true){
Node pre = cur;
if(cur.key > key){
cur = cur.left;
if (cur == null){
pre.left = new Node(key, red, null, null, pre);
checkNode = pre.left;
break;
}
} else {
cur = cur.right;
if (cur == null){
pre.right = new Node(key, red, null, null, pre);
checkNode = pre.right;
break;
}
}
}
// 삽입 후 리밸런싱 하기
reBalance(checkNode);
}
}
public void reBalance(Node node){
// 이중 빨강 조건일 때 while문 작동
while (node.parent != null && node.parent.color == red){
Node sibling = null;
if (node.parent.parent.left == node.parent){
sibling = node.parent.parent.right;
} else {
sibling = node.parent.parent.left;
}
// 조건에 따라 부모 노드의 형제의 색이 빨강, 검은색이나 없을 때로 나누어 작성
if (sibling != null && sibling.color == red){
node.parent.color = black;
sibling.color = black;
node.parent.parent.color = red;
if (node.parent.parent == this.head){
node.parent.parent.color = black;
break;
} else {
node = node.parent.parent;
continue;
}
} else {
if (node.parent == node.parent.parent.left){
if (node.parent.right == node){
node = node.parent;
leftRotate(node);
}
node.parent.parent.color = red;
node.parent.color = black;
rightRotate(node.parent.parent);
} else if (node.parent == node.parent.parent.right){
if (node.parent.left == node){
node = node.parent;
rightRotate(node);
}
node.parent.color = black;
node.parent.parent.color = red;
leftRotate(node.parent.parent);
}
break;
}
}
}
public void leftRotate(Node node){
if (node.parent == null){
Node rNode = this.head.right;
this.head.right = rNode.left;
rNode.left.parent = this.head;
this.head.parent = rNode;
rNode.left = this.head;
rNode.parent = null;
this.head = rNode;
} else {
if (node.parent.left == node){
node.parent.left = node.right;
} else {
node.parent.right = node.right;
}
node.right.parent = node.parent;
node.parent = node.right;
if (node.right.left != null){
node.right.left.parent = node;
}
node.right = node.right.left;
node.parent.left = node;
}
}
public void rightRotate(Node node){
if (node.parent == null){
Node lNode = node.left;
node.left = lNode.right;
lNode.right.parent = node;
lNode.right = node;
node.parent = lNode;
this.head = lNode;
lNode.parent = null;
} else{
if (node.parent.left == node){
node.parent.left = node.left;
} else {
node.parent.right = node.left;
}
node.left.parent = node.parent;
node.parent = node.left;
if (node.left.right != null){
node.left.right.parent = node;
}
node.left = node.left.right;
node.parent.right = node;
}
}
public void levelOrder(Node node){
char[] color = {'B','R'};
Queue<Node> queue = new LinkedList();
queue.add(node);
while (!queue.isEmpty()){
Node cur = queue.poll();
if (cur.left != null){
queue.offer(cur.left);
}
if (cur.right != null){
queue.offer(cur.right);
}
System.out.print("[" + color[cur.color]+ "]" + cur.key + " ");
}
System.out.println();
}
}
public class Practice1 {
public static void main(String[] args) {
// Test code
RedBlackTree rbTree = new RedBlackTree();
rbTree.insert(20);
rbTree.insert(10);
rbTree.insert(30);
rbTree.levelOrder(rbTree.head);
rbTree.insert(25);
rbTree.levelOrder(rbTree.head);
rbTree.insert(5);
rbTree.insert(7);
rbTree.levelOrder(rbTree.head);
rbTree.insert(20);
rbTree.levelOrder(rbTree.head);
}
}
'자료구조' 카테고리의 다른 글
| 자료구조 - 힙(Heap) (0) | 2023.01.04 |
|---|---|
| 자료구조 - 그래프(Graph) (0) | 2023.01.03 |
| 자료구조 - 균형 이진 탐색 트리(Balanced Binary Search Tree) (1) | 2022.12.30 |
| 자료구조 - 이진 탐색 트리(Binary Search Tree) (0) | 2022.12.30 |
| 자료구조 - 이진 트리(Binary Tree) (0) | 2022.12.29 |



